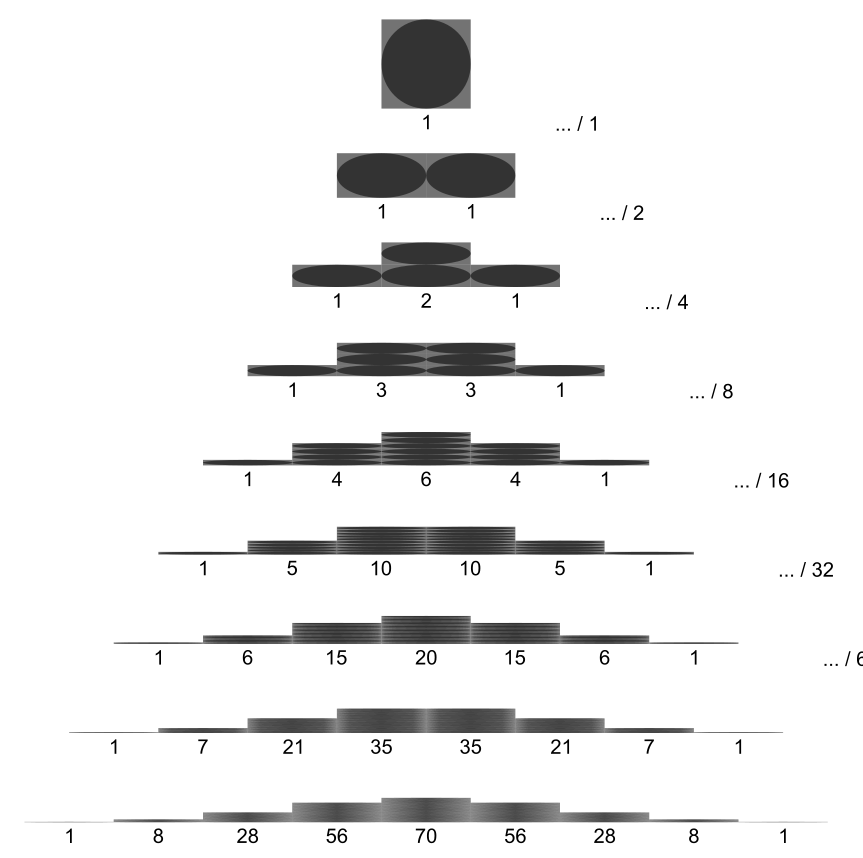
The formula for the binomial distribution only began to resonate with my intuition once I made an analogy between a sequence of Bernoulli trials and arranging items in two types of boxes. Once I made that analogy, it became easier to see problems in those terms. In this post, I want to share that simpler way of looking at the binomial distribution.

The formula for the the binomial distribution is

\begin{equation} P(X = k) = \binom{n}{k} p^k (1-p)^{n-k} \end{equation}

where $n$ is the number of trials, $k$ is the number of successes, $p$ is the probability that any trial is a success, and

\begin{equation} \binom{n}{k} = \frac{n!}{k! (n-k)!} \end{equation}

Let's put this aside for now this for now, and start with something much more basic.

Trials, Successes, Failures

The binomial distribution is applicable when you have a series of trials, and each of those trials can result in a success or a failure. Think of a coin toss. If you toss a coin 5 times, you can consider each toss a trial. These trials are independent of each other; the outcome of any trial has no impact on the outcome of any other. The probability that any event ends in a success is probability $p$, so the probability of a failure on any trial is $(1-p)$.

I don't like thinking in terms of a sequence of events that outcomes described in terms of emotional valence. The binomial distribution is much more generally applicable than for instances of 'success' or 'failure'. It applies any time you have a set of events, objects, or anything that can be categorized into two classes, as long as the probability that any of the events/objects/things in one of those classes is the same for all the events/objects/things.

Suppose we have 7 very intelligent swans, and each swan has a 0.3 probability of solving a math problem. Then the number of swans which solve the problem follows the binomial distribution.

Suppose a couple is planning on having 4 children, and that each child has a 0.25 probability of being red headed. The number of red headed children they will have follows a binomial distribution.

Suppose you are in a large classroom and are wondering how many people in it are playing Pokémon Go. If everyone in the room has a 0.05 probability of playing, the probability of the number of people playing follows a binomial distribution.

Mapping objects/events to numbers

A mathematical formula only becomes useful when you are able to map the real world problem to the formula. In other words, if you can't look at real world problems and see how they can be formulated into a math problem, the math is purposeless. Unfortunately it is extremely difficult to see how a real world problem is exactly the same as the set up for a math problem, and this skill isn't taught very well in schools. This is why most of your friends lack your enthusiasm for math.

For the binomial distribution, the trick is to give every event/object/thing a number. If we have 7 swans let's give each one a number. Our 7 swans will now be called

\begin{equation} 1, 2, 3, 4, 5, 6, 7 \end{equation}

They may honk in protest at the ordering, but more likely they won't even be aware of this dehumanizing (de-swanizing?) label.

All our swans in a row

After giving them all numbers, the next step in seeing the binomial distribution pop out of this problem is to take our clump of swans and put them in a straight line. Then, from left to right, their order could be

\begin{equation} 3, 7, 4, 1, 2, 5, 6 \end{equation}

or

\begin{equation} 7, 6, 5, 4, 3, 2, 1 \end{equation}

or even

\begin{equation} 1, 2, 3, 4, 5, 6, 7 \end{equation}

How many different ways could we do this ordering? This is a very important question. Let's imagine we have 7 boxes in a row, and we're going to put in our 7 swans one at a time from left to right.

How many different choices do we have for the first box? We have 7 patient swans at our disposal, so we have 7 choices. Now, let's make a choice and put lucky swan 3 in the first box.

The swans see what we are up to, and they don't take kindly to being confined in our boxes for a mathematical demonstration. "Use ducks instead!" they honk. Quick! We have to pick our next swan before they get away. How many choices do we have? Well, swan 3 is boxed, so that leaves 6 choices left. What if, instead of swan 3, we had chosen swan 6? In that case, we still would have had 6 choices. This is true no matter which swan we had picked first. For each of the 7 swans we could have chosen for our first box, we would have had 6 remaining choices for the second. So our total number of choices for the first two boxes would be $7\times6$. But we are getting ahead of ourselves. Let's make a choice. 2, come here!

Now, to fill the third box, we have 5 swans remaining, therefore 5 possibilities for the third box. Once we have the third box filled, we have 4 swans left, so 4 choices for the fourth box. And so on, until we eventually have a single swan left for the last box, swan 6. Which one should we put in? We gaze at swan 6, and he gazes back with a look of resignation. He knew what was coming before you did, and knows that the sooner this mathematical demonstration is over with, the sooner he can get back to his very busy social agenda. He waddles over to the seventh box and steps in.

We can consider each choice we made as a branch point in a decision tree. The first choice had 7 possibilities, so 7 branches off of the main trunk. The second choice had 6 possibilities, so each of those 7 branches has 6 branches coming out of them. If we draw this tree all the way to the leaves, and count the number of leaves, we will get the total number of possible decisions we could have made. This is the same as the total number of ways the 7 swans could have been put in the 7 boxes. This number is $7\times6\times5\times4\times3\times2\times1 = 7! = 5040$. The swans are very glad you didn't decide to try out every combination before you were convinced.

In general, if you have $n$ events/objects/things you are trying to arrange, there are $n!$ different ways to do the arrangement. This is the backbone of the logic behind the binomial theorem. Now that you understand this, the rest is easy.

Swan Contest

Let's make our swans a little more excited about being placed in boxes, by giving them a challenge. We will independently ask each one of them a tricky math problem. These swans have been hanging out with us for a while, so they have a much more extensive math background than your average bird. Suppose that for each swan, the probability they get the math problem correct is 0.3. If a swan gets the problem correct, she gets to go into the red box, where we've placed a PB&J sandwich (minus the PB&J).

Suppose swans 2, 3, and 7 get the problem right, while the other four get the problem wrong. Let's put the three winners in three red boxes containing the delicious prize, and the losers in four green boxes.

What is the probability that that particular set of three swans (swan 2, 3, and 7) got the problem right, while the others got it wrong? Because the performance of each swan is independent of the other swans, we just have take the probability that each outcome happened, and multiply those seven numbers together.

\begin{equation} P(\text{swan 1 losing}) \times P(\text{swan 2 winning}) \times \dots \times P(\text{swan 7 winning}) \end{equation}

\begin{equation} 0.7 \times 0.3 \times 0.3 \times 0.7 \times 0.7 \times 0.7 \times 0.3 = p^3 (1-p)^{7-3} \end{equation}

This equation, you'll have observed, looks like the second part of the formula for the binomial distribution. In fact, this is where it comes from. When you have $n$ events/objects/things that can be divided into two categories, and there is probability of $p$ that any single one of them is in the first class, then the probability that a particular set of $k$ of them is in the first class and all the others are in the second class is given by

\begin{equation} p^k (1-p)^{n-k} \end{equation}

We have almost arrived at the binomial distribution! Now that we know how likely it is for swan 2, 3, and 7 to be the only winners, all we need to do is to figure out how many different ways there are for exactly 3 swans to win. If there were 35 different ways exactly 3 different swans could win, then we would add up the probability a particular set of 3 swans win 35 times. In other words, we would multiply $p^k (1-p)^{n-k}$ by 35. So the last question we need to answer is: how many ways are there to chose 3 swans from a set of 7?

Red and Green boxes

We need to figure out how many ways there are to get unique sets of exactly 3 winning swans. We can approach this problem by sorting the swans every possible way, and dividing this by how many 'redundant' orderings we counted. A redundant ordering is one in which the order isn't exactly the same, but the same 3 winning swans are in red boxes. Once we have sorted the events/objects/things into two categories, the ordering within those categories doesn't matter at all. So how many redundant orderings are there? In other words, how many ways are there to mix up the order of the swans without unfairly putting a winner in a bread-less green box?

If only swans 1, 2, and 3 get the math problem correct, we can put them in boxes like this

or like this

We could try to list every possible arrangement of swans that keeps winners in red boxes, but this would take a long time. There must be a systematic way of figuring out how many orderings there are.

Looking at the red boxes by themselves, let's see how many different ways we have placed the same winning 3 swans in the red boxes, but in different orders.

We see that there are $3! = 6 $ ways to order the three swans in the red boxes. And if we mix up all the losing swans in the green boxes:

we have $4! = 24$ different orderings. I probably didn't need to show this to you, as we showed in an earlier section that there are $n!$ ways to order $n$ items. Now, how many ways are there of ordering both the winning swans in the red boxes and the losing swans in the green boxes? We can count every possible pair of possible red-box orderings and green-box orderings. This gives us $3! \times 4! = 144$ different redundant orders.

So, if we try to figure out how many unique sets of 3 winning swans out of 7 total swans there are, we can arrive at the result with the following logic. We order the swans in every possible order, which gives us $7!$ different orders. Then we divide this number by how many times we redundantly counted the same winners in different red boxes and the same losers in different green boxes, which is $3! \times (7-3)!$. So the total number of unique sets of 3 winning swans is:

\begin{equation} \binom{7}{3} = \frac{7!}{3! (7-3)!} = 35 \end{equation}

Binomial Birds

We now have all the pieces to understand the binomial distribution. The binomial distribution tells us the probability that we have exactly $k$ events/objects/things in one of two categories, out of $n$ things total. To find this, we calculate the probability of one particular set of $k$ things being in the first category, which is

\begin{equation} p^k (1-p)^{n-k} \end{equation}

Then we simply take that number and multiply it by how many possible ways there are to chose $k$ things from $n$ things. In our swan example, it was how many unique sets of 3 winning swans there are among 7 swans total. To calculate this, we order the $n$ items in all possible ways, and then divide by how many times we over-counted each unique set: $k! \times (n-k)! $ times.

Putting everything together in equation form, the probability that $k$ things end up in the first category is:

\begin{equation} P(X = k) = \frac{n!}{k! (n-k)!} p^k (1-p)^{n-k} \end{equation}

This is the binomial distribution! We've done it, thanks to our very patient and intelligent swans.