import numpy as np
import scipy
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib
import sys

from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
sns.set_context('notebook', font_scale=1.5)
sns.set_style('whitegrid')
%config InlineBackend.figure_format = 'retina'

import tensorflow as tf
print(f'python version {sys.version[:5]}')
print(f'Tensorflow version {tf.__version__}')
print(f'Eager execution on: {tf.executing_eagerly()}')
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd

if tf.test.gpu_device_name() != '/device:GPU:0':
    print('WARNING: GPU device not found.')
else:
    print(f'SUCCESS: Found GPU: {tf.test.gpu_device_name()}')

python version 3.7.6
Tensorflow version 2.2.0
Eager execution on: True
WARNING: GPU device not found.

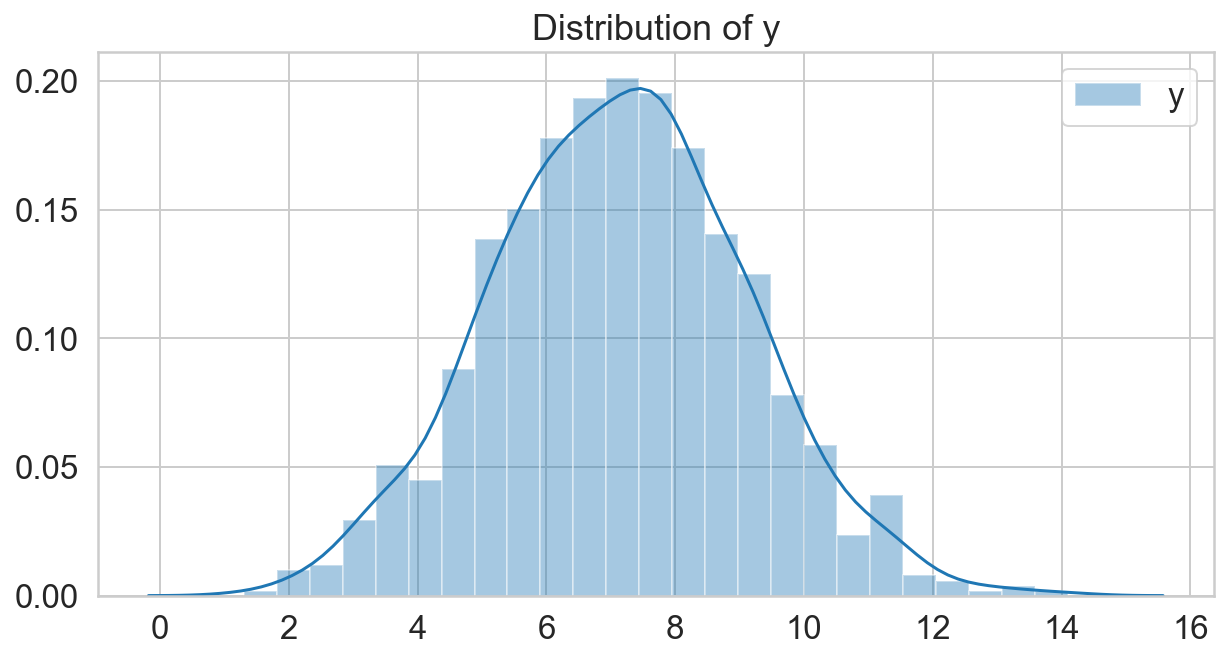
np.random.seed(30)
N = 1000
x_1 = -4.5 
x_2 =  5.5
mu = np.sqrt(x_1**2 + x_2**2)
sigma = 2
y = scipy.stats.norm(mu, sigma).rvs(N)

fig, ax = plt.subplots(figsize=(10, 5));
sns.distplot(y, label='y');
ax.legend();
ax.set_title('Distribution of y');

def unnormalized_log_prob(theta):
    # theta = [sigma, x1, x2]
    sigma = theta[0]
    mu = tf.norm(theta[1:])
    loglikelihood = tf.reduce_sum(tfd.Normal(mu, sigma).log_prob(y))
    logprior = tfd.Exponential(1).log_prob(sigma)
    logprior += tf.reduce_sum(tfd.Uniform(-10, 10).log_prob(theta[1:]))
    logposterior = logprior + loglikelihood
    return logposterior

theta = tf.constant([1, 1, 1], dtype=tf.float32)
logposterior = unnormalized_log_prob(theta)

## Run HMC

starting_state = tf.constant([1, 1, 1], dtype=tf.float32)
num_results = int(1e5)
num_burnin_steps = int(1e3)
adaptive_hmc = tfp.mcmc.SimpleStepSizeAdaptation(
    tfp.mcmc.HamiltonianMonteCarlo(
        target_log_prob_fn=unnormalized_log_prob,
        num_leapfrog_steps=3,
        step_size=1.),
    num_adaptation_steps=int(num_burnin_steps * 0.8))

# Run the chain (with burn-in).
@tf.function
def run_chain():
    samples, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=starting_state,
      kernel=adaptive_hmc,
      trace_fn=lambda _, pkr: pkr.inner_results.is_accepted)
    return samples, is_accepted
samples, is_accepted = run_chain()

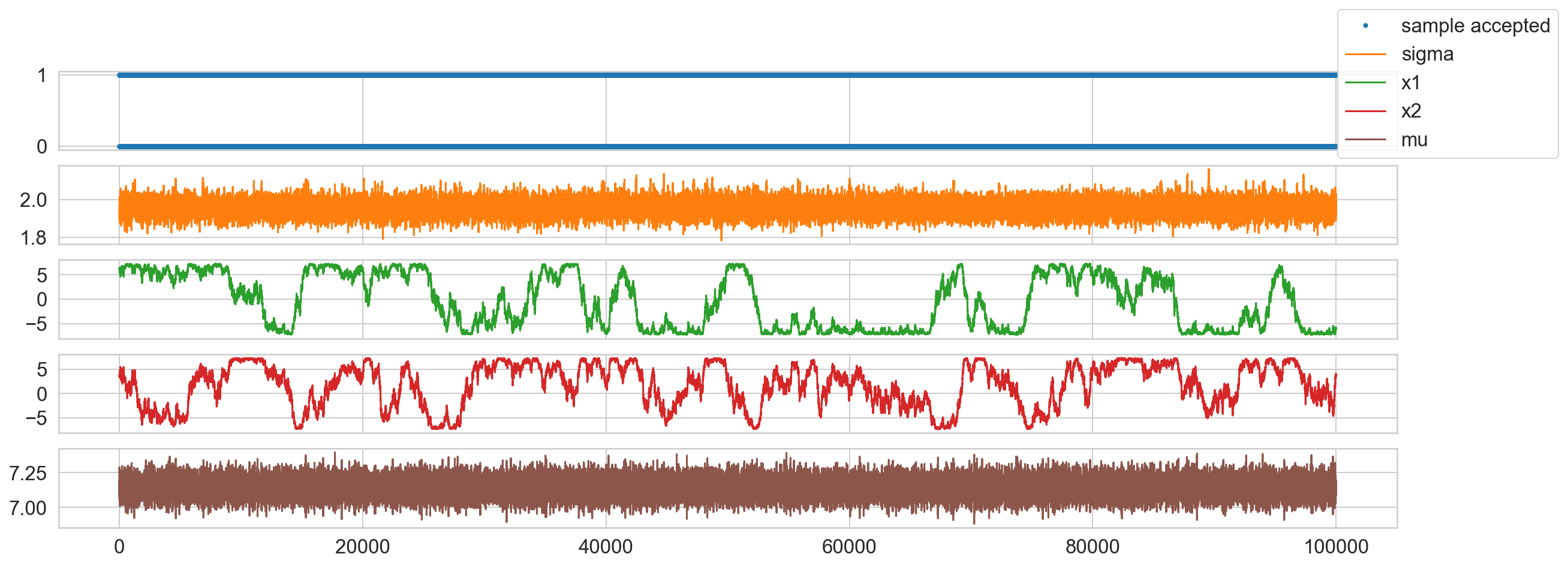
# Plot Samples
accepted_samples = samples[is_accepted.numpy()]
print(f'Accepted samples: {len(accepted_samples):,}/{len(samples):,}')
fig, ax = plt.subplots(5, 1, sharex=True, figsize=(20, 7));
ax[0].plot(is_accepted.numpy(), '.', c=sns.color_palette()[0], label='sample accepted');
ax[1].plot(samples[:, 0], c=sns.color_palette()[1], label='sigma');
ax[2].plot(samples[:, 1], c=sns.color_palette()[2], label='x1');
ax[3].plot(samples[:, 2], c=sns.color_palette()[3], label='x2');

ax[4].plot(tf.sqrt(tf.reduce_sum(samples[:, 1:]**2, axis=1)), c=sns.color_palette()[5], label='mu');
fig.legend();

Accepted samples: 71,781/100,000

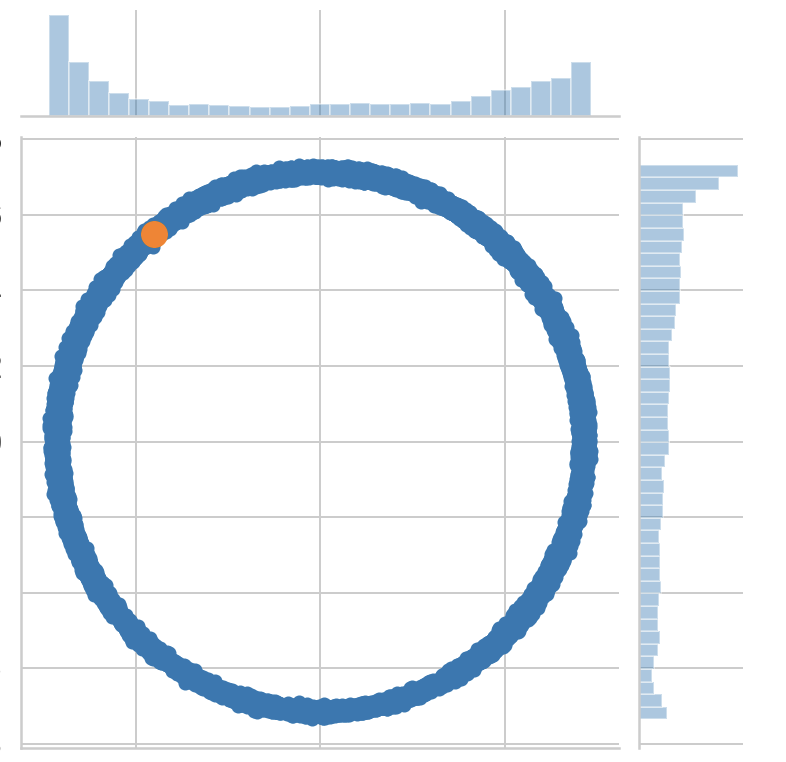
s_sigma = accepted_samples[:, 0]
s_x1 = accepted_samples[:, 1]
s_x2 = accepted_samples[:, 2]
s_mu = np.sqrt(s_x1**2 + s_x2**2)
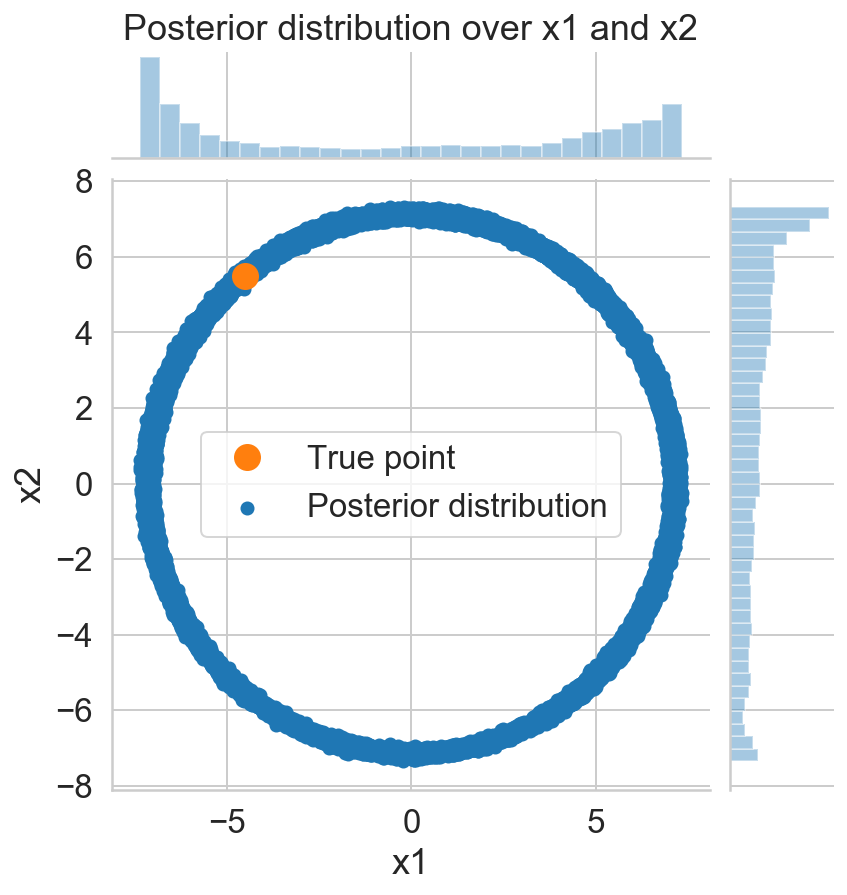
p = sns.jointplot(s_x1, s_x2, label='Posterior distribution');
ax = p.fig.axes[0];
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.plot(x_1, x_2, '.', markersize=25, c=sns.color_palette()[1], label='True point');
ax.legend();
p.fig.axes[1].set_title('Posterior distribution over x1 and x2');

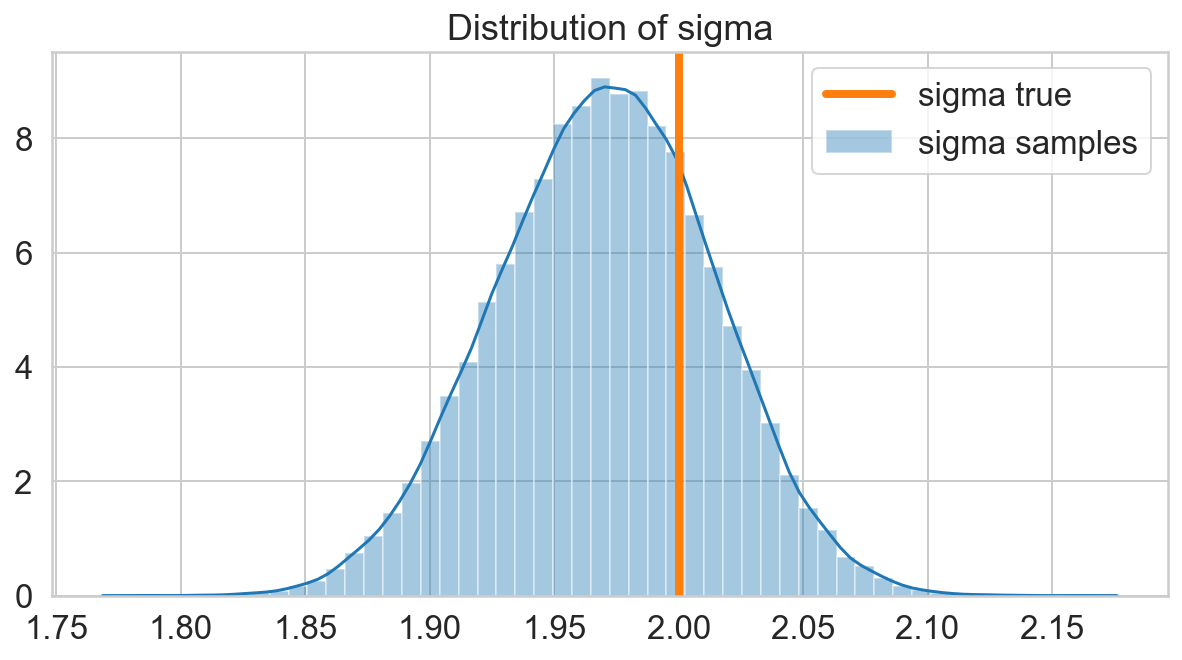
fig, ax = plt.subplots(figsize=(10, 5))
sns.distplot(s_sigma, ax=ax, label='sigma samples')
ax.axvline(x=sigma, lw=4, c=sns.color_palette()[1], label='sigma true')
ax.set_title('Distribution of sigma');
ax.legend();

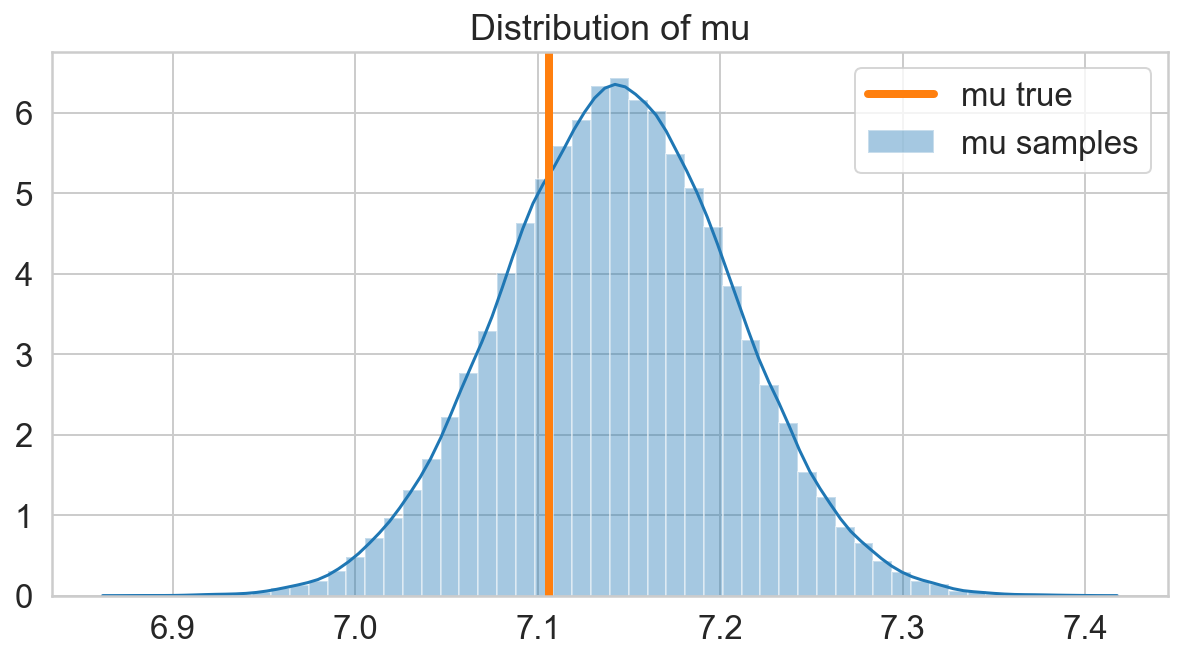
fig, ax = plt.subplots(figsize=(10, 5));
sns.distplot(s_mu, label='mu samples', ax=ax);
ax.axvline(x=mu, lw=4, c=sns.color_palette()[1], label='mu true')
ax.legend();
ax.set_title('Distribution of mu');

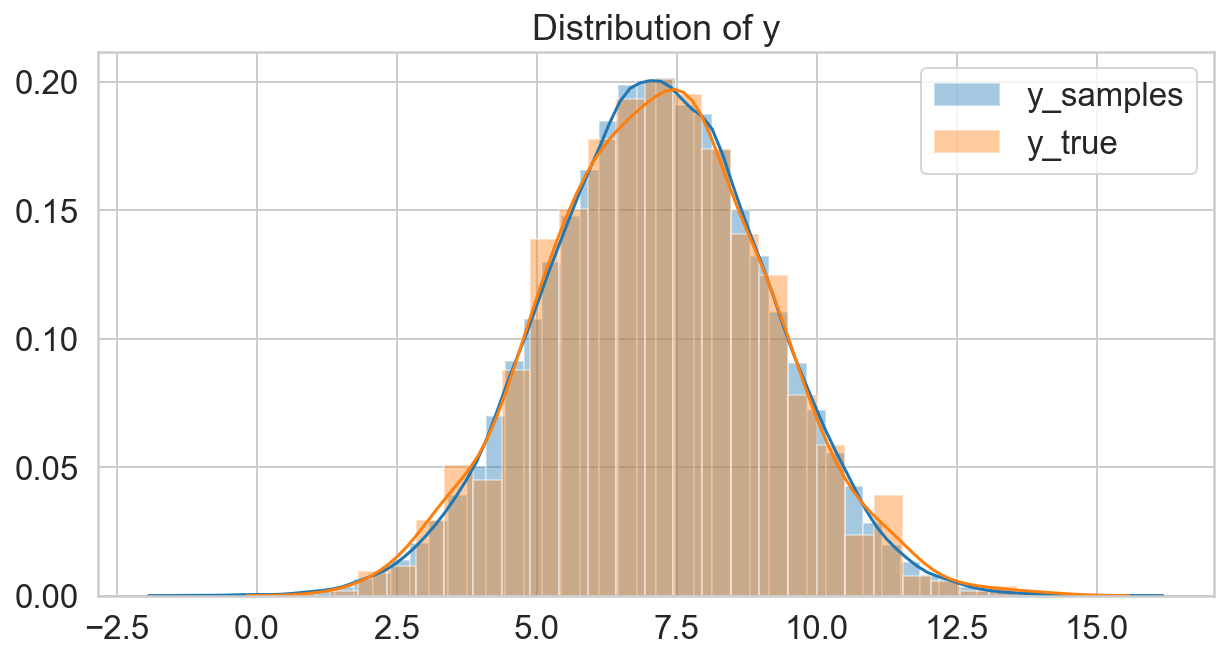
y_samples = scipy.stats.norm(s_mu, s_sigma).rvs()
fig, ax = plt.subplots(figsize=(10, 5));
sns.distplot(y_samples, label='y_samples', ax=ax);
sns.distplot(y, label='y_true', ax=ax);
ax.legend();
ax.set_title('Distribution of y');