Background
In this post I'll go over the Yoneda Lemma, a theorem in category theory. This follows the notation from chapter 23 of "The Joy of Abstraction" by Eugenia Cheng, although the diagrams are my own.
The Yoneda Embedding
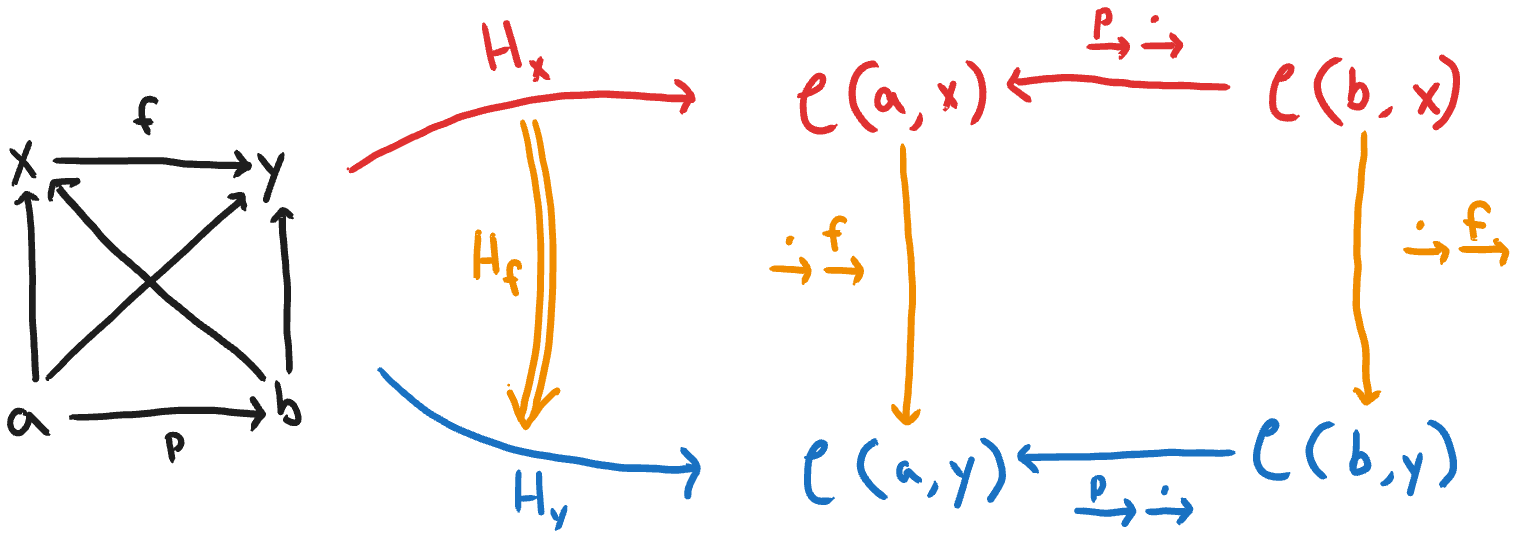
Consider the category \(𝒞\), which has objects \(x, y, a, b\) and morphisms as shown in the diagram. We can fix a particular object \(x\), and consider all the homsets which have \(x\) as the codomain (e.g. \(𝒞(a, x)\), \(𝒞(b, x), ...\)). We can also consider all the morphisms between the domains of these homsets (e.g. \(p\) being a morphism from \(a → b\), where \(a\) and \(b\) are the domains of the homsets in \(Set\)), and see that precomposition with these morphisms form functions between these homsets. Together, this association from objects and morphisms form a functor \(H_x\) from \(𝒞\) to \(Set\).
Since we can do this with any object \(x\), let's construct one of these functors for each object in \(𝒞\). Then let's observe that we can construct a natural transformation between these functors (e.g. \(H_f\) in the above diagram). Each component of this natural transformation is a function between homsets in which we postcompose with a morphism in \(𝒞\). The requirement for natural transformations is that their naturality square (pictured above inside \(Set\)) commutes. We can pick any morphism \(f\) from \(x → y\), use this for all components of the natural transformation \(H_f: H_x → H_y\), and see that the naturality square commutes. This is because, by the associativity axiom of morphisms in the original \(𝒞\), precomposition with \(p\) followed by postcomposition with f (the red arrow followed by the left orange arrow) is equal to postcomposition with \(f\) followed by precomposition with \(p\) (the right orange arrow followed by the blue arrow).
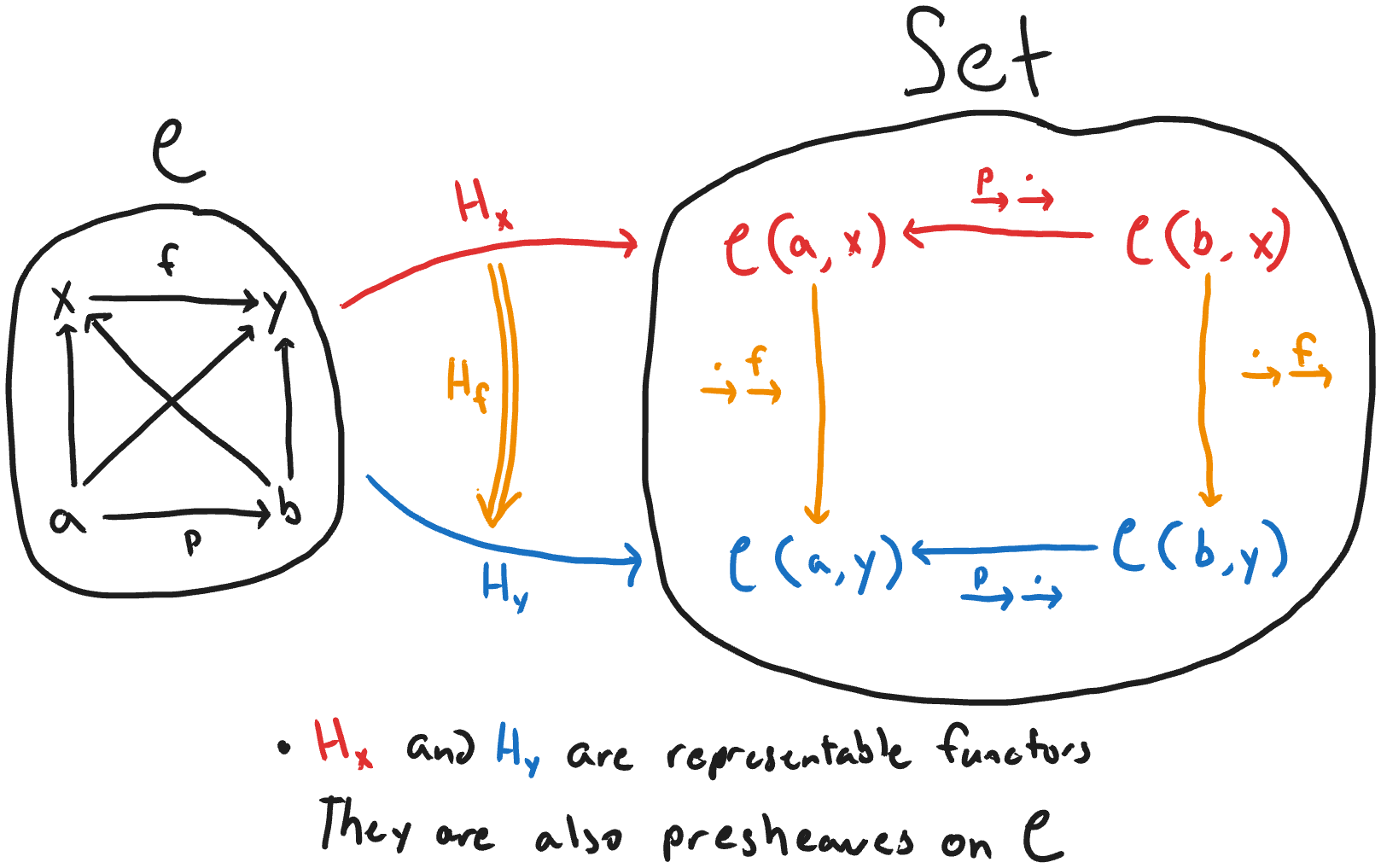
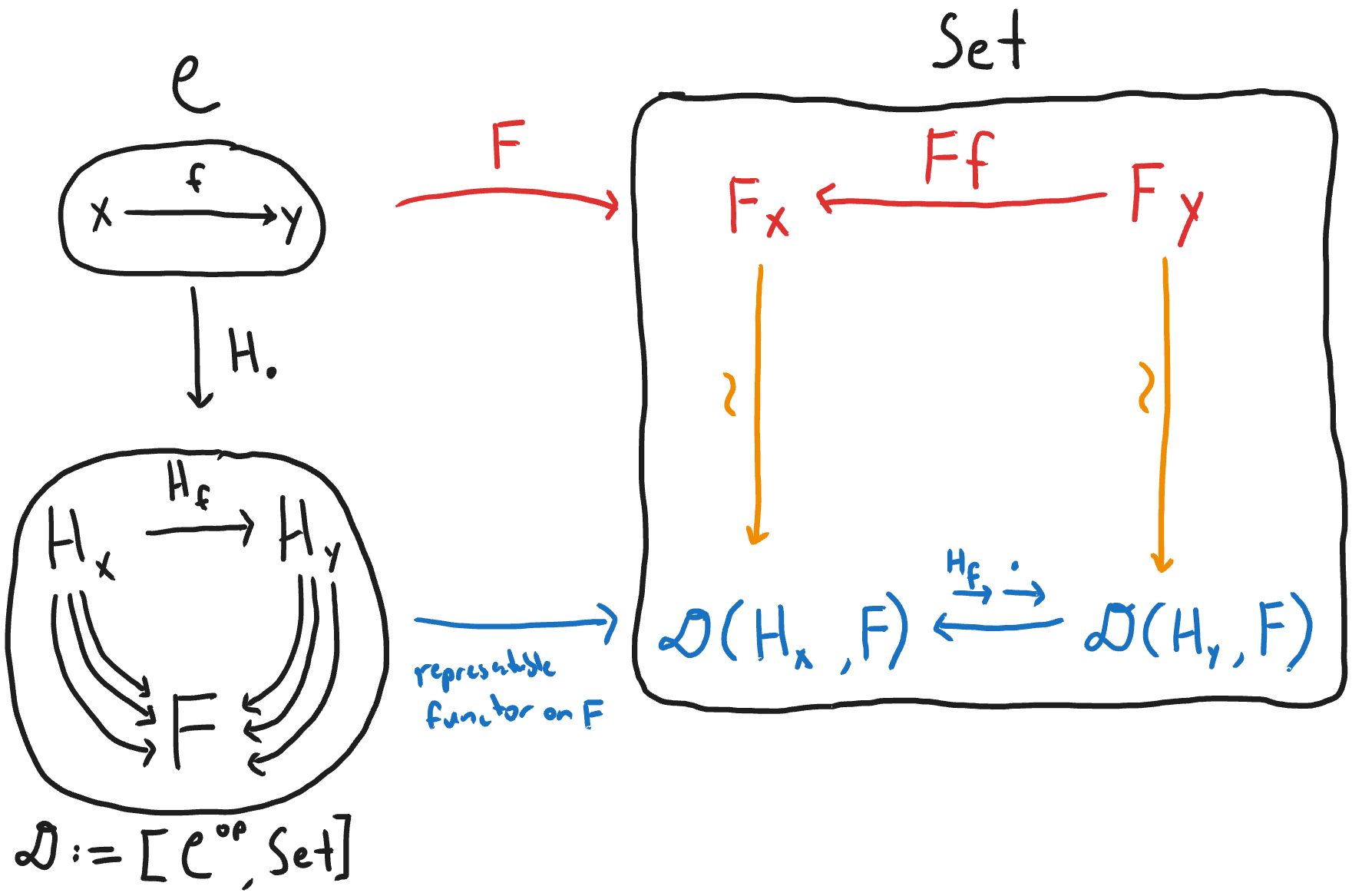
Above we constructed a natural transformation \(H_f\) between the functors \(H_x\) and \(H_y\). In fact, we can construct, for any object in \(𝒞\), a functor (called the representable functor), and for every morphism in \(𝒞\) between those objects, a natural transformation between their representable functors. All these functors are objects in the functor category[\(𝒞^{op}, Set\)]. All these natural transformations between these functors are the morphisms in this category. This is pictured below.
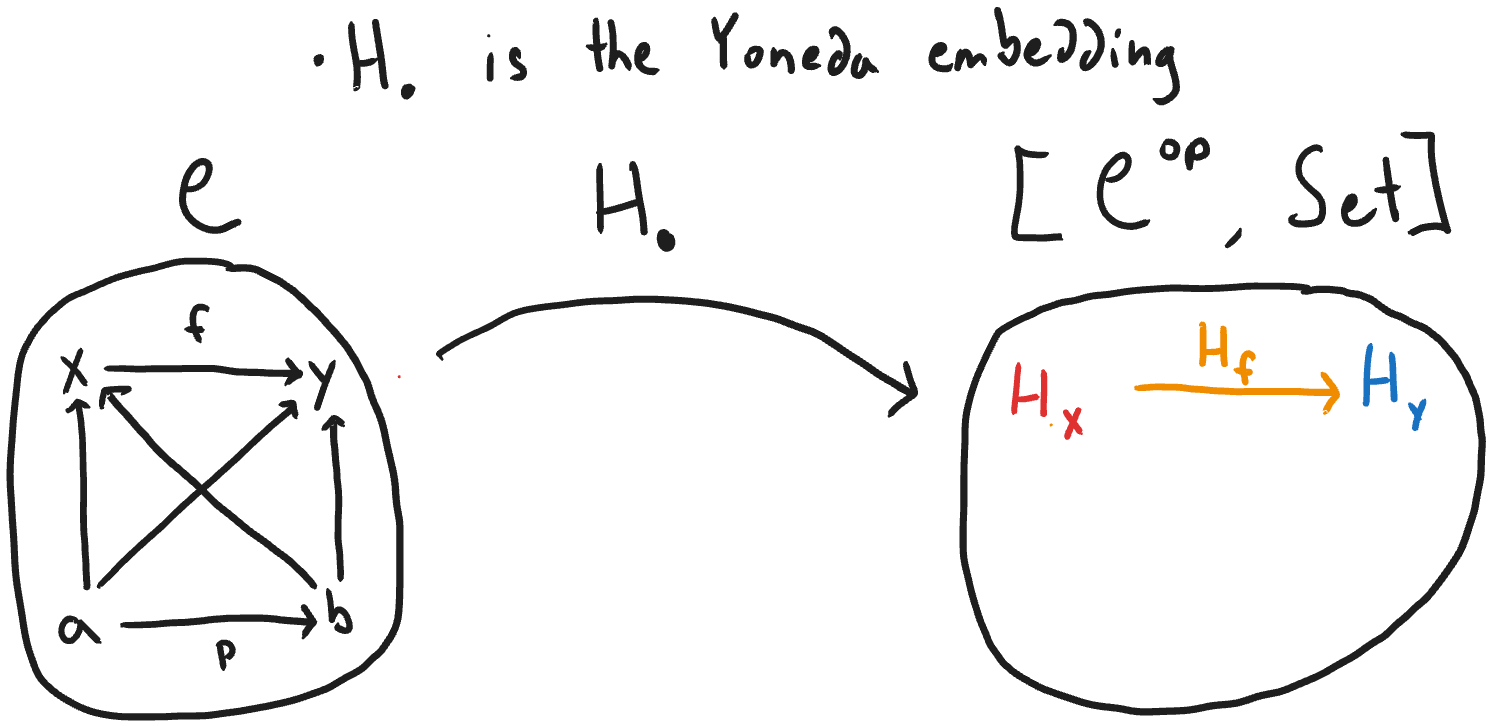
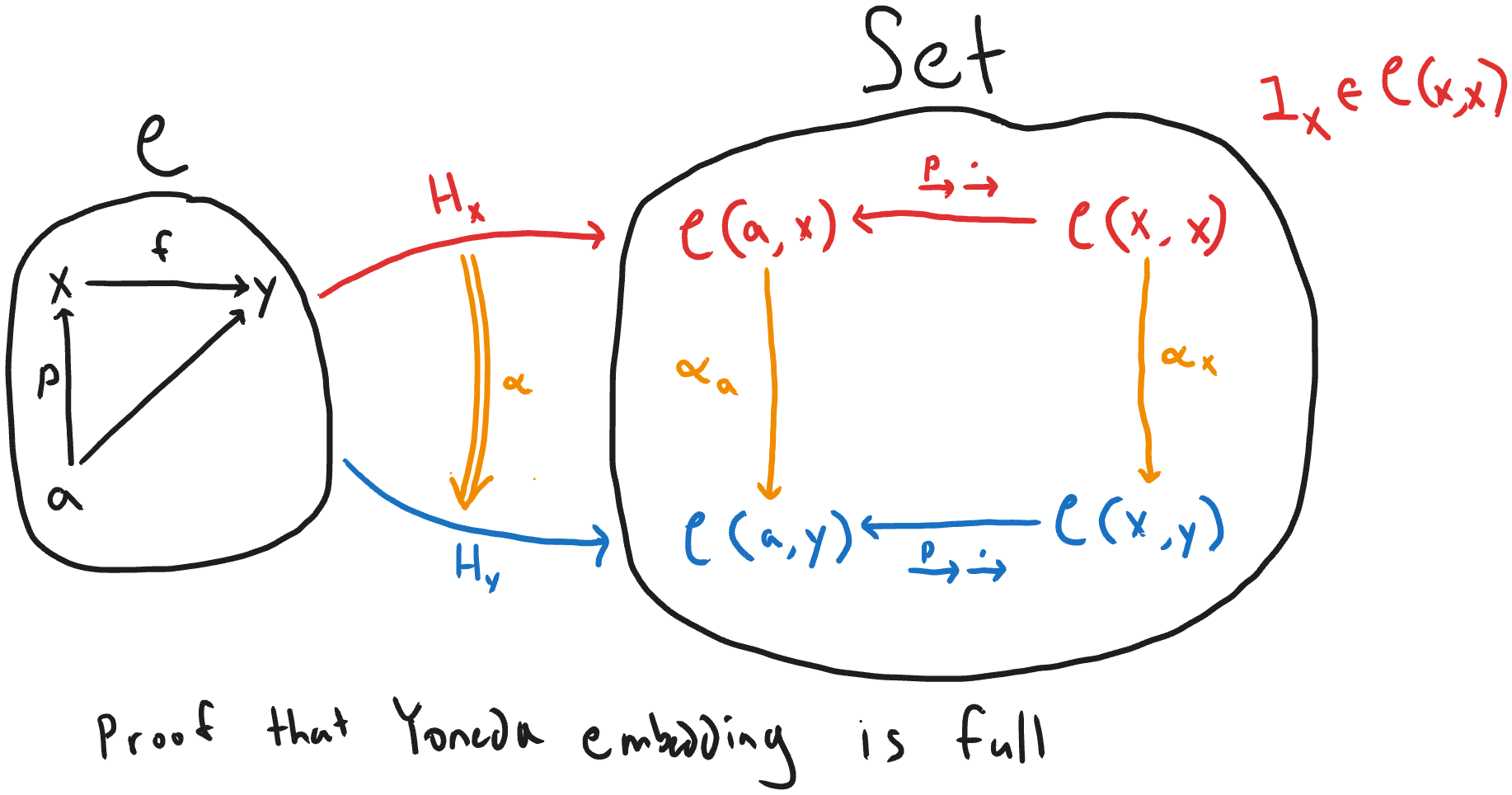
The association of objects and morphisms in \(𝒞\) to functors and natural transformations in \([𝒞^{op}, Set]\) is the "Yoneda embedding" (symbolized as \(H.\)). The Yoneda embedding is full and faithful. To see that it is faithful, consider the diagram below. Suppose there are two morphisms \(f, g\) in \(𝒞\) from x to y such that their natural transformations \(H_f, H_g\) are equal. Then, for any object \(a\) in \(𝒞\), the components of \(H_f\) and \(H_g\) are equal. We can then construct the naturality square as seen inside \(Set\), where the red and blue functions are precomposition with the identity morphism of \(x\). Now consider that \(1_x ∊ 𝒞(x, x)\), and that the naturality square commutes, so that \(f ∘ 1_x = g ∘ 1_x\), so \(f = g\). This shows it is faithful.
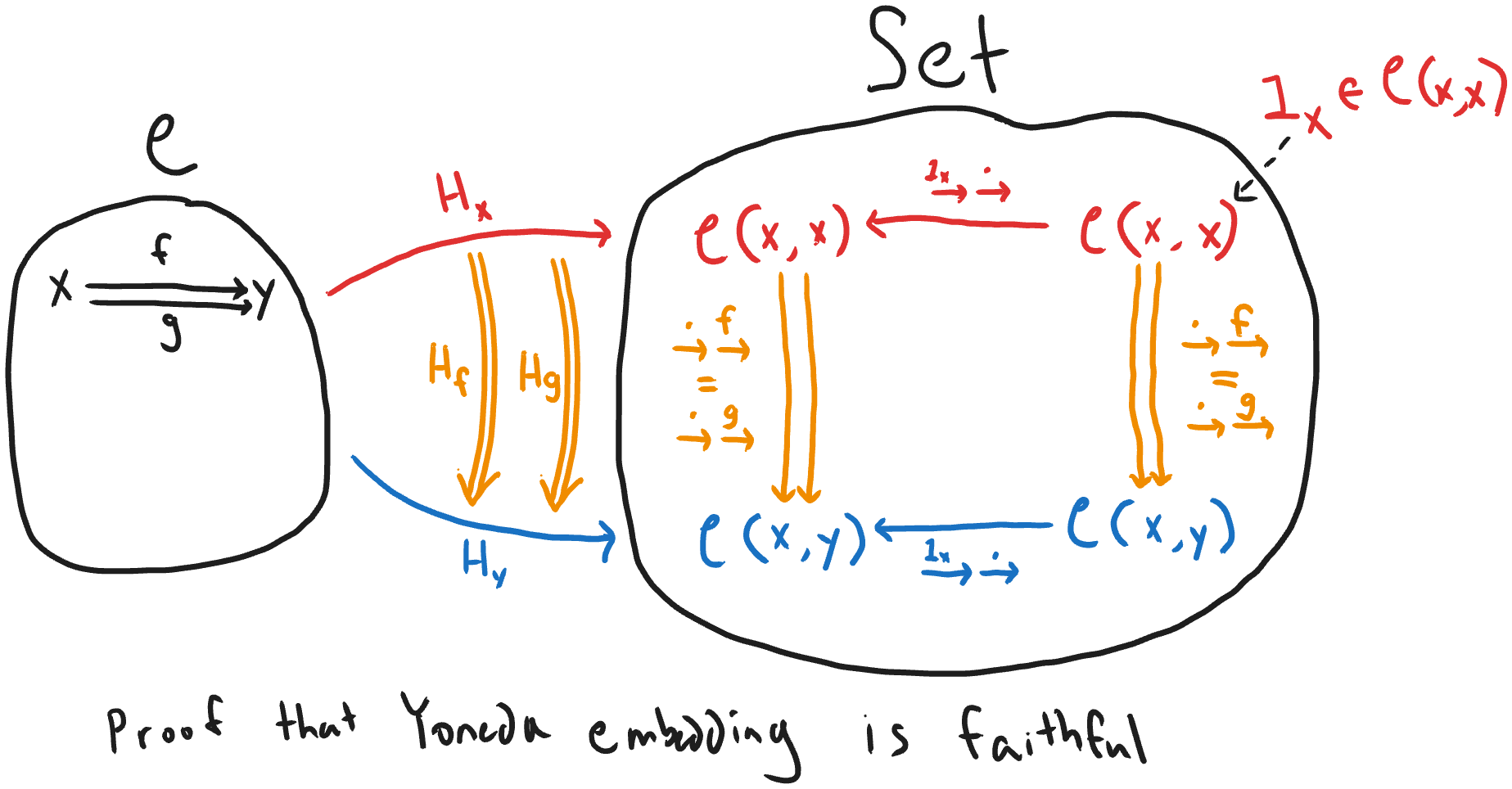
To prove that the Yoneda embedding is full, we need to show that for any natural transformation α: \(H_x → H_y\), there is a morphism \(f: x → y\) such that \(H_f\) (where it gets mapped to by the Yoneda embedding) is equal to α. \(H_f\) is the natural transformation made up of postcomposition with \(f\) at every object, so we need to show that each component of \(α\) is equal to postcomposition with some \(f\). As in the above proof of faithfulness, let's consider the action of \(α\) on \(1_x\), as shown inside \(Set\) in the diagram below. Since the naturality square commutes, we have that precomposition of \(p\) followed by the action of \(\alpha_a\) is equal to the action of \(\alpha_x\) followed by precomposition with \(p\). Or algebraically, \(α_a(1_x ∘ p) = α_x(1_x) ∘ p\). In order to construct the \(\alpha_x\) in the naturality square, there must be a morphism \(f: x → y\), by type checking the homsets (every morphism from \(x\) to itself gets mapped to a morphism from \(x\) to \(y\)). So let's set \(\alpha_x\) to be postcomposition with \(f\). Plugging this into our formula for the naturality square's actions on \(1_x\) becomes: \(\alpha_a(p) = (f ∘ 1_x) ∘ p = f ∘ p\), so \(\alpha_a\) is precomposition with f. This is exactly our definition of \(H_f\), so the Yoneda embedding is full.
The Yoneda Lemma
Now note that there is one representable functor \(H_x\) for each object \(x\) in \(𝒞\). We can think of each one of these representable functors as objects in the category \([𝒞^{op}, Set]\). But there are many other objects in this category that the Yoneda embedding doesn't hit! These other objects are functors from \(𝒞^{op}\) to \(Set\) as well, but don't need to be constructed the way we did for the representable functions (i.e. by mapping objects to homsets and morphisms to postcomposition functions). They can be constructed in arbitrary ways. Let's consider an arbitrary functor \(F\) from \(𝒞^{op}\) to \(Set\). Then there is an isomorphism between \(Fx\) and the set of natural transformations from \(H_x\) to \(F\).
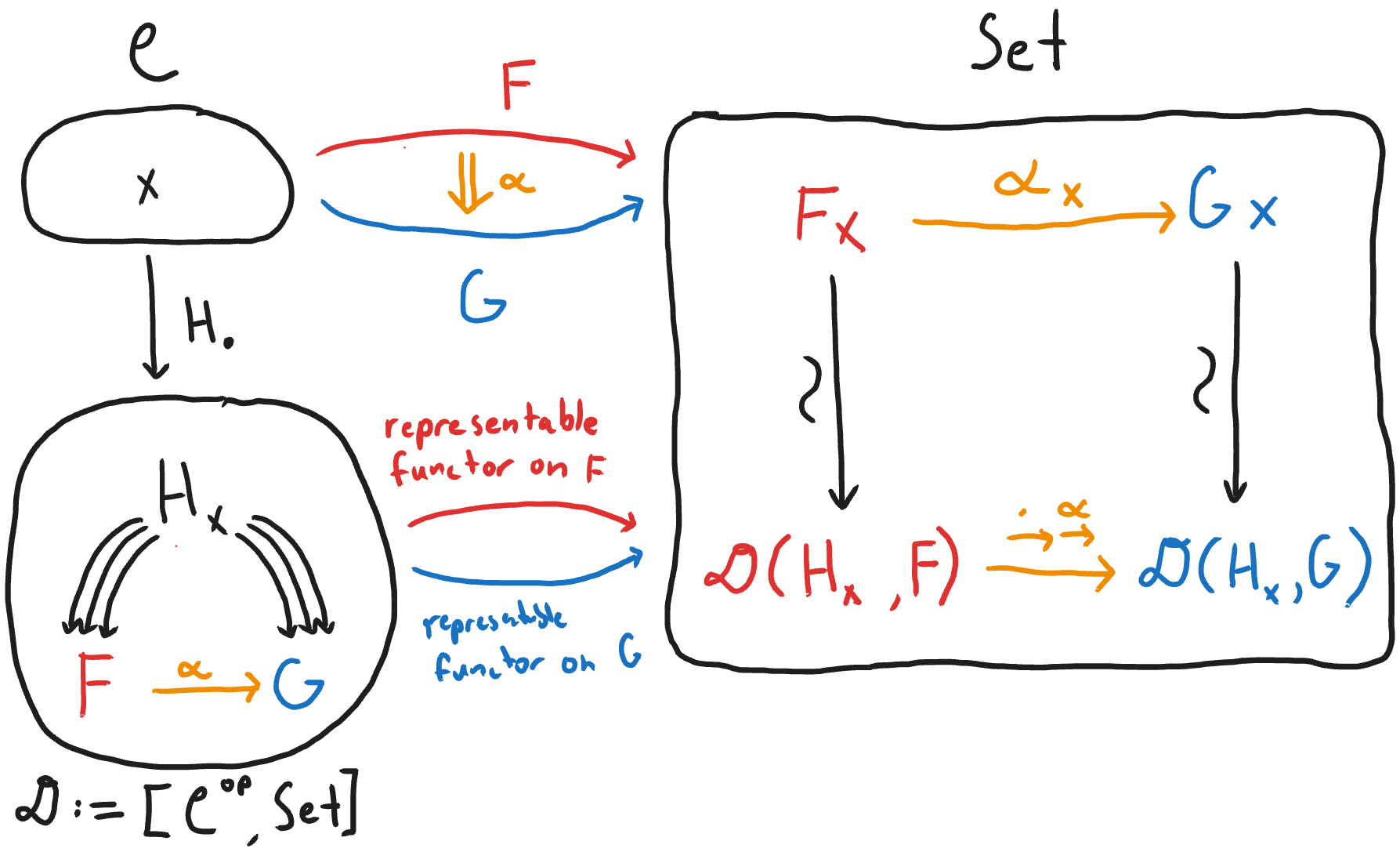
The above is not the full statement of the Yoneda Lemma. I'll edit this post with the full statement once I include the proof.